布隆过滤器-Bloom Filter

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

简介

​ Bloom Filter是由 Burton Howard Bloom在1970提出的，用来判断一个元素是否存在集合中的概率算法。经过Bloom Filter判断过不在集合中的元素就一定不在集合中，若判断结果是在集合中，则可能会误判，即该元素可能不在集合中。换句话说，可能会误判，但绝不可能漏判。元素可以添加到集合中，但不会被删除（尽管可以通过“计数”过滤器来解决）; 添加到集合中的元素越多，误判的概率就越大。Bloom Filter将元素映射到位数组中，所以极大的节省空间。

算法描述

​ 通常我们判断一个元素是否在集合中，可以将集合存放在一个列表等数据结构中，通过比对查找的方式判断是否包含该元素，但是当元素的个数越来越大时，列表占用的内存空间会越来越大，可以将其存放在磁盘空间中，但是这样会大大降低查询时间。进一步改进，可以通过散列表来映射元素到二进制位数组中，真正的数据存放磁盘空间中，内存存放散列表，通过元素散列映射的位是否为1判断元素是否存在集合中。但是散列表当元素增加时，发生冲突的概率也不断增大，冲突会降低查询的效率，为了减少冲突，可以通过多个哈希函数解决，当一个元素通过多个哈希函数映射的位都为1时，那么判断元素可能在集合中，否则元素必定不在元素中。Bloom Filter就是使用这种方法。

初始化

​ Bloom Filter是通过不同的哈希函数映射到位数组，初始化是一个位数组，数组元素全设置为0，代表目前没有元素在集合中，数组的初始化长度下文会介绍。

bit_array

插入元素

​ 插入的元素需要通过k个哈希函数得到k个对应的位数组上的位置，将这些位置上的位全都设置为1，若已经设置为1，则可以不做任何改变。

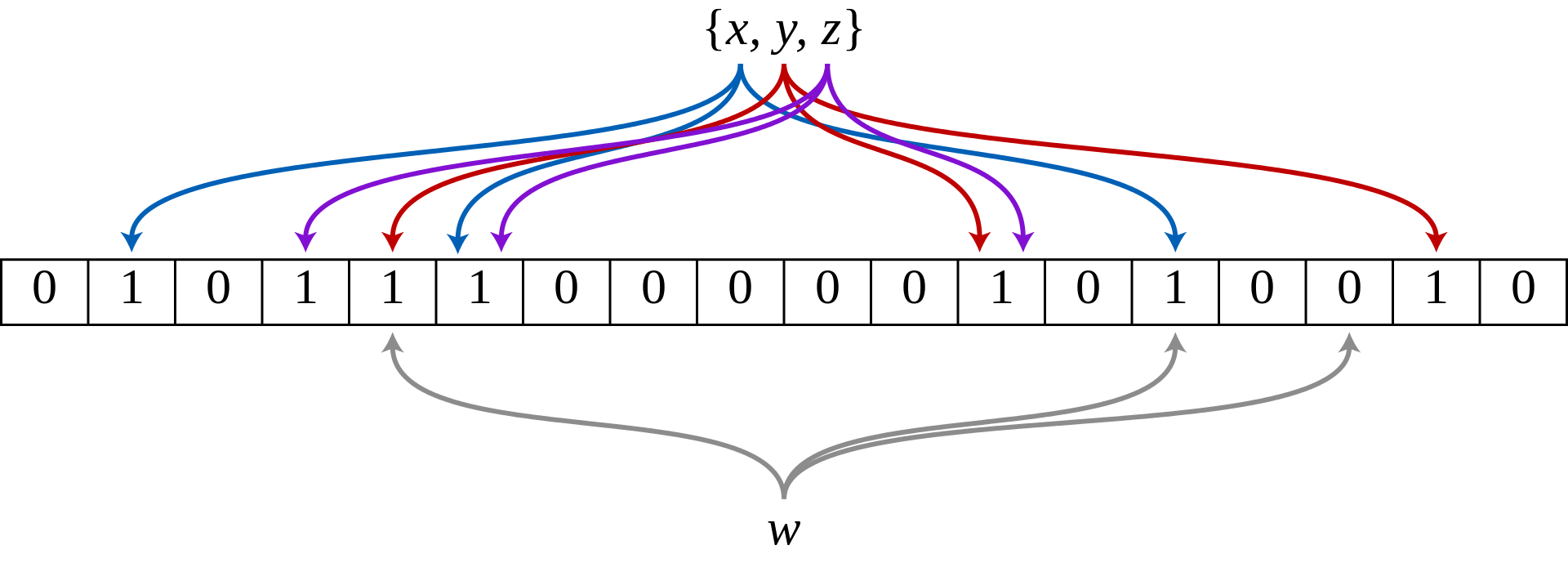
bit_array

如图将集合中的x，y，z通过三个哈希函数得到的位数组上对应的位都设置为1。

判断元素是否在集合中

​ 将需要判断的元素同样通过k个哈希函数得到k个对应的位数组上的位置，判断其位置上的位是否全为1，若是则元素可能存在在集合中，否则必定不存在。如上图的w通过哈希函数得到的位置上的位有一个不为1，则w必定不存在该集合中。

参数的选择

Bloom Filter主要有四个参数:

  • $k$：哈希函数的个数
  • $m$：位数组的大小
  • $n$：集合的元素个数
  • $p$：假阳性概率（false positive probability），即将不在集合中的元素判断为在集合中，误判的概率

哈希函数的数量$k$必须是正整数。如果不考虑这个约束，则对已给定的$m$和$n$或$p$，当$k$满足以下公式时误判的概率最小：
$$
k = -\frac{lnp}{ln2} = \frac{m}{n}ln2
$$
而由$n$和$p$可以得到最佳的$m$的值：
$$
m = -\frac{nlnp}{(ln2)^2}
$$
所以每个元素的最佳位数是：
$$
\frac{m}{n}=-\frac{lnp}{(ln2)^2}\approx-1.44log_2p
$$

实现

Bloom Filter的简单实现，参考：https://github.com/MagnusS/Java-BloomFilter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
import java.io.Serializable;
import java.nio.charset.Charset;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
import java.util.BitSet;
import java.util.Collection;

public class BloomFilter<E> implements Serializable {
    int k;          //hans函数的个数
    int m;          //bit的位数
    int n;          //存储的预期容量
    int size;       //实际存储的容量
    BitSet bitSet;
    static final Charset CHARSET = Charset.forName("utf-8");
    static final String hashName = "MD5";
    static final MessageDigest MESSAGE_DIGEST;
    static {
        MessageDigest tmp;
        try {
            tmp = MessageDigest.getInstance(hashName);
        }catch (NoSuchAlgorithmException e){
            tmp = null;
        }
        MESSAGE_DIGEST = tmp;
    }
    /**
     * 根据假阳性概率和预计个数计算bit数组的大小
     * @param falsePositiveProbability 假阳性概率
     * @param n 预期的集合的个数
     * @return
     */
    private static int calculateM(double falsePositiveProbability, int n){
        return (int)Math.ceil(-1.44*Math.log(falsePositiveProbability)/Math.log(2.0) * n);
    }

    /**
     * 根据假阳性概率和预计个数计算散列函数的个数
     * @param falsePositiveProbability 假阳性概率
     * @param n 预期的集合的个数
     * @return
     */
    private static int calculateK(double falsePositiveProbability, int n){
        return (int) Math.round(calculateM(falsePositiveProbability, n)/ (double)n * Math.log(2.0));
    }

    /**
     * 根据bit数组的大小和预计个数计算散列函数的个数
     * @param m
     * @param n
     * @return
     */
    private static int calculateK(int m, int n){
        return (int) Math.round(m/(double)n * Math.log(2.0));
    }

    public BloomFilter(double falsePositiveProbability, int n){
        this(calculateK(falsePositiveProbability, n), calculateM(falsePositiveProbability, n), n);
    }

    public BloomFilter(int m, int n){
        this(calculateK(m, n), m, n);
    }

    public BloomFilter(int k, int m, int n){
        this.k = k;
        this.m = m;
        this.n = n;
        bitSet = new BitSet(this.m);
        size = 0;
        System.out.println("bloom filter init success, K: " + k + " m: " + m + " n： " + n);
    }

    /**
     * 得到相应的hash
     * @param data
     * @param hashNum
     * @return
     */
    public static int[] getHashs(byte[] data, int hashNum){
        int[] result = new int[hashNum];

        int k = 0;
        byte salt = 0;
        while (k < hashNum){
            byte[] digest;
            synchronized (MESSAGE_DIGEST){
                MESSAGE_DIGEST.update(salt);
                salt++;
                digest = MESSAGE_DIGEST.digest(data);
            }

            for(int i = 0; i < digest.length/4 && k < hashNum; i++){
                int h = 0;
                for(int j = i*4; j < (i*4) + 4;j++){
                    h <<= 8;
                    h |= ((int) digest[j] & 0xFF);
                }
                result[k] = h;
                k++;
            }
        }
        return result;

    }

    /**
     * 添加元素到过滤器中
     * @param element
     */
    public void add(E element){
        int[] hashCodes = getHashs(element.toString().getBytes(CHARSET), this.k);
        for(int hashCode: hashCodes){
            bitSet.set(Math.abs(hashCode % this.m), true);
            size ++;
        }
    }

    public void addAll(Collection<E> collection){
        for(E element: collection){
            add(element);
        }
    }

    /**
     * 判断元素是否在集合中
     * @param element
     * @return
     */
    public boolean contains(E element){
        int[] hashCodes = getHashs(element.toString().getBytes(CHARSET), this.k);
        for(int hashCode: hashCodes){
            if(! bitSet.get(Math.abs(hashCode % this.m))){
                return false;
            }
        }
        return true;
    }

    public boolean containsAll(Collection<E> collection){
        for(E element: collection){
            if(! contains(element)){
                return false;
            }
        }
        return true;
    }
}

应用

  • 爬虫中的url去重
  • Hbase中通过Bloom Filter来快速确定查询的数据是否在HFile中，加快查询速度
0%